Special Topics in Computer Graphics

References:

1. Dick Oliver, "FractalVision - Put Fractals to Work for You", Sams Publishing, 1992.

Up to this point we have covered some of the basic fundamentals of computer graphics: Drawing pixels to a buffer, 3D polygon and camera coordinates specifications, lighting & shading models, texture maps, etc. This page looks at some special topics that go beyond the basics, and at some of the followup courses students may want to take next.

• One of the most important conferences and groups in the general field of computer graphics is ACM SIGGRAPH, which is the Special Interest Group on Graphics for The Association for Computing Machinery. Online the SIGGRAPH home page may be found at http://www.siggraph.org/, whose conference proceedings are available through the ACM Digital Library.

Fractals

• The basic idea of fractals are to apply a mathematical equation or algorithm to produce a structure with infinite detail no matter how closely you zoom in, and in many cases to generate pretty pictures as a result.
• One of the simplest and most common fractals is the Sierpinski triangle, which starts with a simple equilateral triangle and recursively sub-divides it, ( theoretically infinitely ) to generate an object with a finite area but an infinite boundary.
• A variation on the Sierpinski Triangle is the Koch Snowflake, which again starts with an equilateral triangle, but recurses by replacing each line segment on the current version of the snowflake with a four-segment replacement having a triangular "bump" in the center of the original line segment.
• Perhaps the most famous set of fractals is the Mandlebrot Set, generated by recursively applying a simple mathematical function to points in the complex plane:

1. Define the region in the complex plane to be searched. The entire Mandelbrot set is contained within the space +/- 2.0 +/- 1.5 j. ( The letter j is used for the complex square root of -1 to avoid confusion with the incrementation variable i to be used shortly. ) Define also the resolution with which to sub-divide the space.
2. For each point in the space:
   1. set Z_0 equal to X + Yj.
   2. Apply the recursion relation Z_i = ( Z_i-1 )^2 + Z_0, until either the new Z_i exits the circle of radius 2.0 centered about the origin, or until the maximum number of iterations has been exceeded, ( counting the number of iterations required as the recursion progresses. )
   3. Color the pixel according to how many iterations it took to exit the circle, usually using a mod function into a list of colors if the point exited the circle, and black otherwise.
3. Based on the resulting image, select a new smaller region to examine, and repeat the process.
4. All those points for which the regression never leaves the circle define the Mandelbrot set. It can be shown that this set has infinite amount of detail, no matter how small an inspection area you choose to look at.

• Joulia Sets are related to Mandelbrot sets. See the above web pages for further details.
• In the field of computer graphics, fractals can be used to generate realistic looking ferns, trees, mountains, clouds, and many other natural looking phenomenon:

Scientific Visualization

• Moved to a separate page.

Animation

• We have included some motion in CS 488, however the Computer Animation course, CS 527, includes a much more in-depth look at this particular aspect of Computer Graphics, including many of the human factors issues dealing with how humans perceive motion. Andy has not taught that course since 2001, but Andy Johnson's CS 527 pages are still on line.
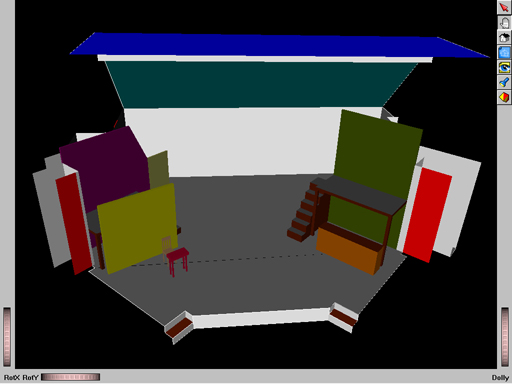
• One example of an animation project from CS 527 is the theatre animation project, designed to plan and simulate set changes for a small local theatre:

Virtual Reality

moved to a separate page

Human-Computer Interaction

• Very often in computer graphics the overall goal is to have some effect on a human, and in order to do that most efficiently, it is important to understand the human side of the equation, and the interaction between the computer and the human. The CS 522 course focuses on this interaction, including input devices such as mice, keyboards, and special devices as well as effective computer graphics displays. Most recently this course has been taught by Tom Moher, but Andy Johnsnon's CS 522 pages from 1998 are still available online ( from when the course was taught as EECS 578. )
• A somewhat related course is CS 422, User Interface Design. This course focuses more on the practical aspects of developing an effective user interface for a particular application, as opposed to 522 which focuses more on the current and historically important research in the field. Andy Johnson's CS 422 pages are available online, and he is scheduled to teach the course in Spring 2006.
• The predominant conference in CHI is the CHI conference, whose home page may be found at http://www.chi2006.org/ and proceedings via the ACM Digital Library.

Game Development

• Jason Leigh teaches an excellent course in "Video Game Design and Programming", which appears officially on the CS course descriptions as "CS 426 - Multimedia Computing". Jason's CS 426 pages are currently online, but do not have a separate URL. To find them, go to Jason Leigh's Home Page, and follow links to "Extra", and then "Classes I Teach". CS 426 is usually taught in the Fall semester.

GPU Programming

• Modern Graphics Processing Units, GPUs, have developed incredible power, often out-performing the CPUs that drive the main computer. In addition, they are specially designed to perform operations on the entire contents of large buffers with a single instruction, which provides opportunities for some very interesting parallel processing applications using these secondary processors. In Spring of 2006 Andy Johnson will be teaching a new ( experimental? ) course in how to effectively use GPUs, titled CS 594, Special Topics. Andy Johnson's GPU Programming course pages are currently online, though they are still preliminary as of this writing.
• Interested parties may also want to check out NVidia's web site, and in particular NVidia's Developer's site, where you can find SDKs for programming NVidia GPUs, and full documentation on how to do so.