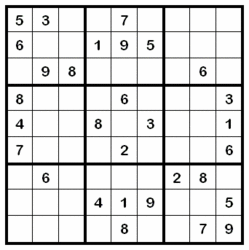
Sudoku is a puzzle that often uses a 9x9 grid of 81 squares.
The grid is divided into rows, columns and boxes. The boxes
are 3x3 sub-grids of 9 squares. Thus each row, column and box
contains 9 squares. The object is the fill in the numbers from
1 to 9 so that each row, column and box contain each number from
1 to 9 only once. For more information, check out the
wikipedia entry
for Sudoku. Note that the wikipedia uses the term "region"
instead of "box".
The following is an example of such a puzzle.

When solving a sudoku puzzle, the solver attempts to find a situation that will resolve (or help resolve) a value in a square. For this assignment, you are to write in C/C++ a Sudoku solver only needs to find the following situations as defined in the Step-by-Step Guide to Solving Sudoku by Angus Johnson.
The general algorithm that most solvers use (and that will be expected for this program) is to begin with a list of all possible values (i.e. 1 through 9) in each square of the grid. This list is often called the candidate list. As each square is resolved, remove that value from the candidate list for the squares that share a row, column or box with the square that is resolved. For a nice application that can show a Sudoku puzzle being solved check out Sudoku Solver by Logic. You can step thought the resolution of all 81 squares using this page. The default puzzle on the page will show examples of recognizing the situations of singles, hidden singles/values and locked candidates.
A single is when a square, X, only has one posible value, V, because the other values are already resolved in a square that share a row, column or box with X. In the puzzle at the top of the page, the square in the vary center of the puzzle (row 5, column 5) must have the value of 5 since the values 1,2,3,4,6,7,8 and 9 are already known in squares that share the row, column or box with the square at row 5, column 5.
This situation is easy to recognize using candidate lists. When an unresolved square anly has a single value in its candidate list, you have a single.
A hidden single is when a square, X, must have the value V because
no other square in a row, column or box could have that value.
Consider the following puzzle.
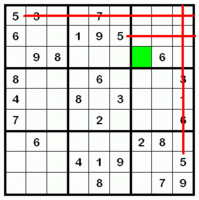
The green square at row 3, column 5
must contain the value of 5 because no other
square in the upper right box could contain the value of 5.
The top row of the box is prevented from having a 5 because of
the 5 at row 1, column 1. The second row of the box is prevented
from having a 5 because of the 5 at row 2, column 6. The right
column of the box is prevented from having a 5 because of the 5
at row 8, column 9. The box can't have a 5 at row 3, column 8 since
it is known to have a 6.
This situation is recognized by checking the canditadate lists for all squares in a group (a group can be a row, a column or a box). If a value only appears in only one candiate list for a group, that value must be the value for the square that corresponds to this candidate list.
This situation will not resolve the value in a square but will reduce the number of possible candidate values for a square.
This situation involves two groups (where a group is a row, column or box) that have three intersecting squares. The possible groups could be:
Consider the following example. The value of 3 in the fifth row
must occur in the first 3 squares (the middle sub-row in the green box).
Thus the value of 3 can be removed from the candidate lists of all
the squares in the top sub-row and the bottom sub-row of the green box.
Once this has been done, the square at position (6,1) should only have
the value of 4 in its candidate list and can be resolved. After that
is resolved, the square at position (4,1) should only have the
value of 5 in its candidate list and can be resolved. The data for
this puzzle is available in proj1data5.txt.
1
2
3
6
8
4 6
7 9
5
7
9
3
This situation will not resolve the value in a square but will reduce the number of possible candidate values for a square.
When a group (row, column or box) has two squares that have the same two value candidate list those two values must exist in those two squares. Those two values can be removed from any other candidate lists in the group.
Consider the following example. The candidate lists for the two green
squares are both (4,6). The candidate list for the red square is
(2,4,6,8). The candidate list for the blue square is (4,6,8).
The green squares have a naked pairs situation. Since the green
squares have the values of 4 or 6 we can remove those values
from the candidate list for all squares in the same group (the
fifth row in this case). By removing the value of 4 and 6 from
the blue square, its candidate list will only have the single value
of 8 and can be resolved. Now, the red square will have had the values
of 4 and 6 removed by the naked pairs and the value of 8 removed
by the single value, so it will have only a single value of 2 left
in its candidate list and can be resolved. The data for this
puxxle is available in proj1data4.txt.
2
8
1 3
5
7
9
2
8
2
Once the puzzle is read in, the initial state of the puzzle is to be displayed to standard output in a 9x9 grid. The squares that need to be resovled should listed with a period.
When the program has finished working on the puzzle, it is to display a message to standard output whether the puzzled was completely solved or not and then it is to print out the final state of the puzzle. This will be done by printing the puzzle in a 9x9 format. If the puzzle was not completely solved, the squares that still need to be resolved should be listed with a period as was done with the initial state of the puzzle.
Your program is also to allow a flag of -v on the command line to put the program in verbose mode. When run in this mode, your program is to print out to standard output some message about each situation that is being resolved. If the puzzle is solved by the program, somewhere around 81 messages would be displayed. This message must specify the situation that is being resolved, the row and column of the square(s) involved and the value(s) involved. If this command line value is not given, this information should not be displayed by your program.
Your program is also to allow a flag of -o on the command line. When this flag is used the final state of the puzzle is to be written to a file. The filename would be given as the command line argument immediately following the -o flag. The format of this output should be the same as the format used to read in a puzzle (an ASCII text file that will have 3 values per line: a row position, a column position and a value).
Your program is also to allow a flag of -h on the command line. When this flag is used the final state of the puzzle is to be written to an HTML file. When this file is opened by a browser, a properly formed 9x9 Sudoku puzzle will be displayed. The filename would be given as the command line argument immediately following the -h flag. It is suggested that an HTML table is used to display the Sudoku puzzle.
Note that all three flags can be given in any order.