| Home |
An assignment in my first programming course in 1971 was to host a party on the computer. Rowell Huesmann, our professor (and a student of Herbert Simon), devised this psychological variant of Conway's Game of Life. A "room" was divided into "cells" where each "guest" could stand. Each guest had a gender and a charisma value. On each iteration of the simulation, each guest would stay put or move to a different cell depending on which guests were standing in surrounding cells. Our task was made doubly difficult by having to implement the program in PL/I and by having to use a card reader.
After I built my Cromemco microcomputer seven years later, one of the first programs I implemented in assembly language was Life. The machine had a fast, high-resolution video board, so I was able to watch colonies of cells glide across the screen like a video game.
Life was fun, stimulating, a metaphor for thinking about the world. I kept it in my algorithm toolkit, waiting to use cellular automata for something practical. I kept a copy of Toffoli and Margolus (1987) on my bookshelf for future reference.
Then I read Stephen Wolfram's A New Kind of Science. This book is more than a metaphor. First, Wolfram explores exhaustively one-dimensional nearest-neighbor automata. Then he moves to higher dimensions and more complex automata. Then he relates automata to almost every scientific field, from biology to psychology to physics. Unlike much of the popular writing on chaos and fractals, Wolfram provides (in copious notes and online resources) proofs, programs, and demonstrations. You can visit www.wolframscience.com for more information.
A cellular automaton is an algorithm for generating a set of cells, given another set of cells. A one-dimensional automaton generates a row of child cells given the pattern in a row of parent cells. The following figure illustrates how this works. It is Wolfram's Rule 1, the first shown in the applet above.
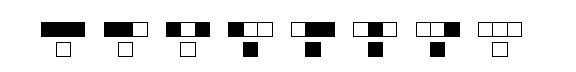
A New Kind of Science will provoke controversy among scientists for years. It has annoyed some mathematicians and scientists because it lacks a bibliography and makes some sweeping claims that have yet to be verified. And some, such as researchers at the Santa Fe Institute who have been working on these problems for years, have tended to be overlooked in the sweep of publicity.
It will take many years to assess whether cellular automata provide a better model for phenomena that scientists now explain through other systems. The word "better" in the last sentence is loaded. It means, among other things, "simpler" (in the sense of Occam's razor), more "predictive" (in the sense of accuracy), "richer" (in the sense of extensibility). These are not absolutes, however. Models can be too simple, fit sample data too well, or be indiscriminately extensible. Scientists' comfort with the models they are using is no excuse for rejecting radically new models, however.
I am not a biologist, so I cannot evaluate Wolfram's claims for biology. But I do collect shells. I compared the pattern on my Conus textile specimen with Rule 18 (Random Seed). Looks pretty similar to me.
Buy the book. At somewhere around $9 a pound, it is probably the best deal you'll find in publishing.
Toffoli, T., and Margolus, N. (1987). Cellular Automata Machines. Cambridge, MA: MIT Press.
Wolfram, S. (2002). A New Kind of Science, Champaign, IL: Wolfram Media, Inc.