Label Layout

NP-hard describes a class of algorithms that require more than polynomial time to reach a solution. Proving label layout is NP-hard is beyond the scope of this note, but we can get an idea by counting combinations. Imagine a simple layout of labels around three points. Assume each point has four possible locations to put a label:

To layout labels, we need to try combinations of label locations in order to avoid collisions. Here is one example of colliding labels: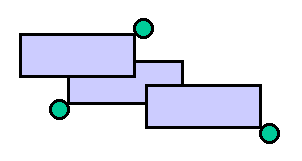

To avoid collisions, we must check all four potential label locations around each point. With three points, that means (worst case) 4 x 4 x 4 = 64 possible locations. And for n points, that means 4ⁿ possible combinations. We denote the order of magnitude of this calculation as O(kⁿ).

The expression n⁴ is a polynomial function of n, but 4ⁿ is an exponential function of n. Here is a graph of both functions:

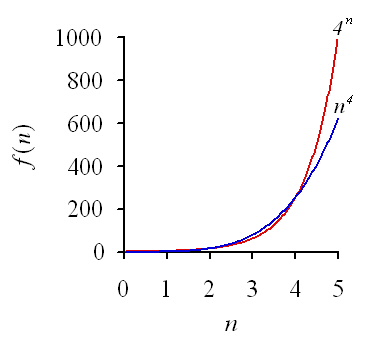
Clearly, O(kⁿ) is going to keep us waiting a long time if n gets large. If we had only 50 points, and each check took us one nanosecond, it would take us over a trillion years to find a solution. We would like to find an algorithm that requires fewer steps.

First of all, if there exists a non-overlapping layout for a given set of points, it would be easy to verify that a layout algorithm has reached a solution (assuming we don't care if a text box occludes a point). Simply visit all pairs of text boxes and examine whether any two boxes overlap. This verification requires n²/2 steps, or O(n²). Checking for a non-overlapping solution can thus be done in polynomial time. However, if we consider the general problem of finding the best possible layout for a set of points and labels (a minimum number of overlaps), we cannot verify if a solution is the best possible unless we compare it with all other solutions. This makes the general labeling problem NP-hard, worse than polynomial because it is O(kⁿ).

There are practical alternatives to exhaustive search. One is to use heuristics, or ad hoc methods that are tailored to approach a satisfactory solution, if not the best. Another method is to construct a badness-of-fit measure (e.g., the total number of overlaps) and try to minimize it using optimization methods. If we are willing to give up the goal of guaranteeing a global optimization, we can search the solution space for points that yield substantial improvements from a random assignment of labels.

A particularly effective method is called simulated annealing. This method is patterned after a physical model - the annealing of a sword or other piece of metal. We decrease temperature in stages and do random searches within stages to try to improve our objective function (badness-of-fit). Although we always accept search states which lead to improvement in the objective function, we are more willing to accept temporary setbacks at higher temperatures. In other words, we are more willing to take one step backward (in the hopes of taking two steps forward) when we are in the early stages of our computations. Later, as we approach the best solution we can find, we become more restrictive in accepting setbacks. More precisely, our propensity to accept a setback decreases exponentially with temperature.

The annealing method works surprisingly well with apparently intractible NP-hard optimization problems. Unlike gradient-based search methods, it is willing to look farther afield in trying possible candidates for a solution. You can read more about simulated annealing elsewhere and in the reference below. Try pressing the Reset button above several times. Notice the behavior of labels on the edge of the frame. It takes a while for the algorithm to notice them, but eventually, with reasonable probability (set by the parameters) they are moved inside the frame. The example above contains 100 points. If we aren't too fussy, there isn't an English word for counting how many years we can save (well, about half a googol, actually).

One more thing. The default annealing algorithm involves randomly choosing a rectangle and checking all other rectangles for overlaps. Instead of fruitlessly examining rectangles at opposite sides of the field, however, we can save time by looking only in a reasonable neighborhood of a rectangle for others that might collide. This cuts the solution time at least in half. This strategy is included in the applet above.

Christensen, J., Marks, J., and Shieber, S. (1995). An empirical study of algorithms for point-feature label placement. ACM Transactions on Graphics (TOG), 14, 203-232.